Les différents paramètres de position pour une variable quantitative
Objectifs
- L'objectif de ce chapitre est de se familiariser avec les deux grands types de paramètres que sont les paramètres de position et les paramètres de dispersion
Les paramètres dits de position sont au nombre de trois :
-
La moyenne
-
La médiane
-
Le mode

La moyenne
Définition

-
Nous ne verrons que la moyenne arithmétique.
-
La moyenne arithmétique d'une série statistique est la moyenne ordinaire, c'est-à-dire le rapport de la somme d'une distribution d'un caractère statistique quantitatif discret, par le nombre de valeurs dans la distribution.
-
De plus, la distribution de ce caractère statistique peut présenter des valeurs répétées un certain nombre de fois. Chaque valeur du caractère de cette distribution sera affectée du coefficient de répétition.
-
On parle alors de moyenne arithmétique pondérée.
Méthode : Méthode de calcul
-
Soit alors x1, x2......xn ,les valeurs prises par le caractère quantitatif étudié auprès des individus constituant la population ou l'échantillon étudié. Soit n1, n2,.....,ni les effectifs correspondants à chaque valeur du caractère quantitatif et N = n1+ n2+.......+ni, l'effectif total de la population ou l'échantillon étudié.
-
La moyenne arithmétique pondérée s'écrit alors :
-
Formule de la moyenne arithmétique pondérée :
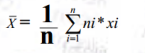
-
Or, on a vu que :
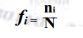
- Par conséquent, la moyenne pondérée peut s'écrire aussi :
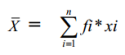
- Si, par contre, pour chaque valeur de xi, l'effectif ni est unique la formule donnant la moyenne arithmétique se simplifie et s'écrit :
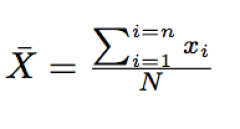
Remarque :
- D'autre part, si les informations sont fournies avec des classes statistiques, on utilisera la même formule en retenant comme valeurs xi, les milieux de classes.
Exemple :
- Pierre au cours de son année scolaire de l'an passé a obtenu dix notes aux épreuves de contrôle de mathématiques. Soit le tableau suivant :

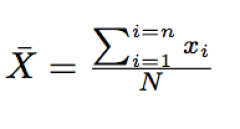
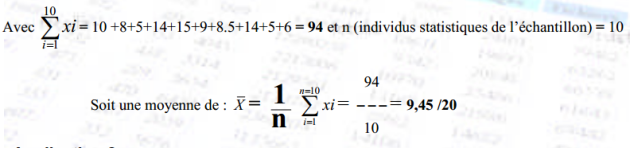
Autre Exemple : la moyenne arithmétique pondérée
-
Une infirmière vient de ranger dans son poste de soins un certain nombre de seringues de différents volumes
-
Soit alors le tableau récapitulatif suivant :

- On utilise, ici, la moyenne arithmétique pondérée pour connaître le volume moyen que représente l'ensemble des seringues rangées dans les divers tiroirs situés au sein d'un poste de soins :
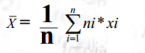
Ici,
-
xi représente les différentes valeurs prises par la variable quantitative : volume de la seringue : On a 2 ml ; 5ml ; 10 ml ; 20ml ; 50 ml.
-
ni représente le nombre de fois que le caractère de la variable quantitative : volume de la seringue est répété.
-
Le caractère 2ml est répété 8 fois ; le caractère 5ml est répété 11 fois ; le caractère 10 ml est répété 5 fois ; le caractère 20 ml est répété 6 fois et le caractère 50 ml est répété 4 fois.
-
Ainsi, on obtient le calcul suivant :
(8 * 2 ml) + (11 * 5 ml) + (5 * 10 ml) + (6 * 20 ml) + (4 * 50 ml) = 441 ml
-
On divise ce résultat, soit 441 ml au total, par le nombre total de fois n, c'est à dire le nombre total de seringues : 8 + 11 + 5 + 6 + 4 = 34 seringues.
-
On a 441/34 = 12, 97 ml en moyenne par unité de seringue.
La médiane
Définition
- La médiane, Me, est la valeur du caractère pour laquelle la fréquence cumulée est égale à 0,5 c'est-à-dire 50 %
Remarque
Il faut distinguer deux cas :
-
Si le caractère est quantitatif discret
-
Si le caractère est quantitatif continu
Méthode : Méthode de calcul
-
Pour un caractère quantitatif discret
-
On commence par ordonner les n valeurs de la série statistique par ordre croissant.
1.Si n est impair
-
la médiane est la valeur de rang : (n+1)/2
-
Elle correspond donc au centre de la série statistique classée par ordre croissant ou à la valeur pour laquelle 50% des valeurs observées sont supérieures et 50% sont inférieures.
2.Si n est pair
- Les valeurs de rangs n/2 et (n/2) + 1 détermine un intervalle médian. Par conséquent, on retient, le plus souvent comme médiane le milieu de l'intervalle de rang : [n/2 ; n/2 +1]
Application
1.Soit la série de 10 notes : 10 8 5 14 15 9 8.5 14 5 6
-
On commence par ordonner les 10 notes. On a : 5 5 6 8 8.5 9 10 14 14 15
-
Le nombre total de notes est 10, donc un chiffre pair
-
De ce fait, la médiane retenue est la valeur du milieu de l'intervalle de rang : [n/2 ; n/2 +1] Ici on a : [10/2 ;10/2 +1] = [5 ;6]
-
La médiane se situe donc entre la 5 ième et la 6 ième note soit entre la valeur 8,5 et 9 du caractère de xi.
-
Soit, maintenant, la même série de 10 notes avec une note supplémentaire 18. On a un nombre impair de notes.
-
Une fois ordonnée on aura la série : 5 5 6 8 8.5 9 10 14 14 15 18 La médiane est la valeur de rang (n+1 /2) = (11+1)/2 = 6, soit la valeur 9 du caractère xi.
Méthode : Méthode de calcul
-
Pour un caractère quantitatif continu
-
La médiane est le nombre m tel que la fréquence cumulée jusqu'à m soit égale à 0.5.
Exemple : Application
-
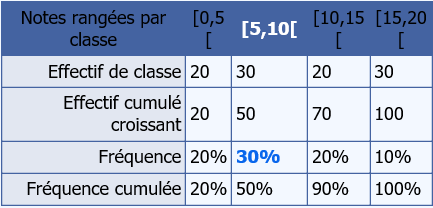
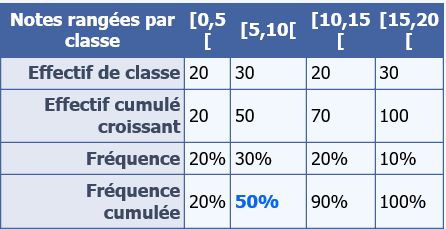
Soit le tableau suivant : nombre de notes à l'épreuve écrite du dernier concours à l'IFSI :
-
La médiane ici est le nombre m situé dans la classe pour laquelle la fréquence est égale à 0,5 soit [5,10[
Le mode
Définition
-
Le mode, Mo, dans le cas d'une série statistique discrète est la valeur du caractère la plus fréquente ou dominante dans l'échantillon.
-
Dans le cas d'une série statistique continue, le mode correspond à la classe de fréquence maximale dans la distribution des fréquences.
Exemple : Application :
-
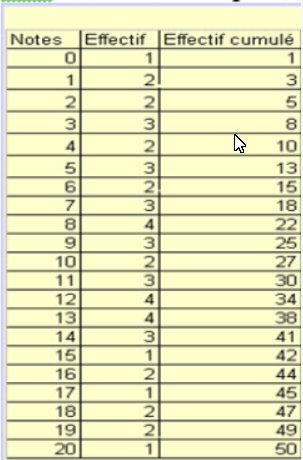
Pour une série statistique discrète :
-
Le mode est la valeur Mo de plus grand effectif, Ici, c'est 8, 12 et 13. On dit que cette série est plurimodale ou trimodale.
-
Pour une série statistique continue :
-
Ici le mode est la valeur Mo correspondant à la classe de fréquence maximale, soit ici 30%. On dit que la classe modale est [5,10[.