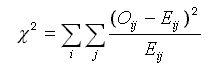Le test du KHI-2

Introduction

• Nous aborderons seulement le test du KHI-2 d'indépendance et le test du KHI-2 d'homogénéité.

• Même si la méthode et la formule de calculs du KHI-2 sont identiques, tant pour le test du KHI-2 d'indépendance que pour le test du KHI-2 d'homogénéité, il existe, cependant, une différence fondamentale dans la manière de choisir les deux variables.

• En effet, on dit que l'on va réaliser un test du KHI-2 d'indépendance lorsque les deux variables qualitatives étudiées sont prises de manière aléatoires, c'est-à dire qu'elles ne sont pas contrôlées par l'investigateur.

• Ainsi, on cherche, par le biais de ce test à connaître, si ces deux variables indépendantes, au départ sont corrélées, liées, en relation entre elles.

• Par contre, on dit que l'on va réaliser un test du KHI-2 d'homogénéité, lorsqu'une des deux variables est contrôlée par l’expérimentateur.

• Dans ce cas, on cherche à savoir si la distribution des effectifs d'une variable est identique ou pas au sein des diverses modalités de l'autre variable.

• Autrement dit, on se pose la question suivante : est ce que la distribution des diverses modalités de la première variable est homogène au sein des diverses modalités de l'autre variable ?.

Le test du KHI-DEUX d'indépendance ou d'homogénéité

Définition

• Un test du KHI-DEUX est une méthode utilisée dans le domaine de la statistique pour vérifier ou non la relation de deux caractères qualitatifs

Condition d'utilisation

• Le test du χ² ne peut s'utiliser que lorsque le statisticien veut étudier la relation ou pas entre deux caractères qualitatifs. Ce test ne s'utilise jamais pour étudier la relation ou pas de deux caractères quantitatifs. Le statisticien fait appel à un autre test : le test de régression linéaire simple avec calcul d'un coefficient : le coefficient de corrélation linéaire. R. Nous ne l'aborderons pas.

• Nous rappelons, de nouveau, la différence sémantique à réaliser entre un test du KHI-2 d'indépendance et un test du KHI-2 d'homogénéité.

• Dans un test du KHI-2 d'indépendance, les deux caractères qualitatifs étudiés sont aléatoires. L'investigateur ne contrôle ni l'un , ni l'autre. Dans ce cas de figure, par le biais de ce test , l’expérimentateur essai de connaître l'existence ou non d'une relation entre ces deux caractères qualitatifs indépendants.

• Dans un test du KHI-2 d'homogénéité, un des deux caractères est contrôlé par l'investigateur. Pour ce cas de figure, l'expérimentateur essaie d'analyser s'il existe une homogénéité ou pas des diverses modalités de l'une des deux variables au sein des diverses modalités de l'autre variable. Si l'on observe une hétérogénéité, alors, il existe une relation entre ces deux variables. Elles sont, par conséquent, liées.

• Pour comprendre ce test, nous allons nous appuyer sur un exemple simple.

Comparaison de la couleur des yeux et des cheveux

• On a recensé les résultats de 6800 personnes classées d'après la couleur de leurs yeux et celle de leurs cheveux.

• On est en présence de deux variables qualitatives : les cheveux et les yeux

• A chacune de ces variables qualitative, on va étudier un caractère qualitatif, respectivement, "la couleur des yeux" et « "la couleur des cheveux »

• Ici, les deux variables ne sont pas contrôlées. On prend 6800 personnes et on regarde la couleur de leurs yeux et de leurs cheveux. C'est un test du KHI-2 d'indépendance

**Méthode pour la réalisation du test du KHI-DEUX

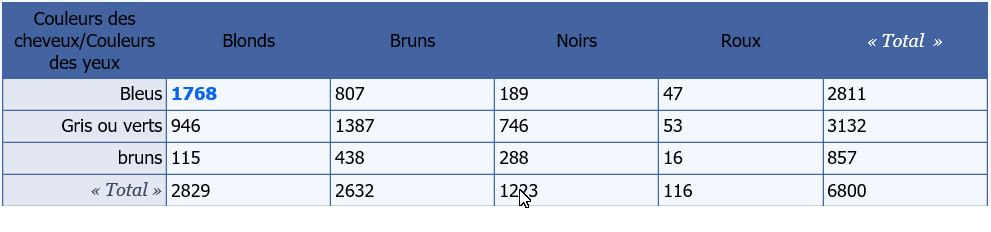
1.Repérer les différentes modalités de chaque variable.

• Pour les cheveux : Blonds, Bruns, Noirs, Roux (quatre modalités)

• Pour les yeux : Bleus, Gris ou verts, Bruns (trois modalités)

2.Vérifier que l'on est en bien en présence de deux caractères qualitatifs ici, nominaux : le premier, la couleur des cheveux, le second, la couleur des yeux.

• Le test du χ² peut donc s'appliquer. Le statisticien veut savoir s'il existe une liaison, c’est-à-dire une relation statistique entre la couleur des cheveux et la couleur des yeux ou bien si ces deux caractères sont indépendants c'est-à-dire n'ont aucune relation ou lien entre eux. Ce test, vous le trouverez dans les logiciels statistiques sous l'appellation de « « tri croisé » »

• On l'appelle tri croisé, car on va trier les valeurs et les ordonner sous la forme d'un tableau dit « tableau de contingence » c’est-à-dire un tableau contenant des lignes et des colonnes. Ici, nous avons trois lignes et quatre colonnes. On note L = 3 et C= 4 (Ligne : L et Colonne : C)

3.On va ensuite croiser les informations fournies par ces deux variables aléatoires qualitatives.

• A l'intersection de chaque ligne et de chaque colonne (case) on observe une valeur : par exemple à l'intersection entre Blonds et Bleus on peut lire la valeur : 1768. Toutes ces valeurs sont des valeurs que le statisticien a relevées lors de l'examen de 6800 personnes. On observe 12 cases de valeurs, hors totaux.

• Avant de réaliser le test du χ², le statisticien va devoir calculer les valeurs théoriques qu'il aurait dû observer, si les deux caractères qualitatifs étaient strictement indépendants. Il obtiendra ainsi 12 valeurs théoriques

• De plus, pour que ce test soit valide, il faut que toutes les valeurs théoriques calculées soit supérieures ou égal à 5. Si tel n'est pas le cas, ce test ne peut s'appliquer. Il ne serait pas valable, c'est-à-dire pas fiable.

Remarque

• l'objectif du test est de comparer chacune des valeurs observées à leur valeur théorique pour apprécier si l'écart, c'est-à-dire la différence entre les valeurs observées et les valeurs théoriques est significative.

• Ce test du χ² donnera au statisticien une valeur qu'il comparera à une « valeur seuil » fournie par une table appelée table du χ².

Fondamental : Trois notions complémentaires fondamentales à connaître pour l'utilisation et l'interprétation d'un test du KHI-DEUX.

Le statisticien a besoin de connaître les trois notions ci dessous énumérées :

1.Le risque d'erreur de premier espèce α

2.Le degré de liberté (ddl)

3.le degré de signification ou encore appelé p-value :p

Exemple : Comment calculer les valeurs théoriques encore appelées valeurs attendues : la couleur des cheveux et des yeux

• Pour chaque case, on multiplie la valeur marginale de la fin de ligne où se situe la case avec la valeur marginale de la fin de colonne correspondant à la valeur observée étudiée et l'on divise le résultat obtenu par le total de l'échantillon N.

• Valeur théorique de chaque case =(total ligne*total colonne)« en correspondance avec la valeur de la case pour laquelle on veut savoir la valeur théorique »/total général.

• Pour exemple, pour la valeur de la première case : 1768 ; la valeur théorique attendue serait de (en cas de véritable indépendance des deux caractères qualitatifs) :

                         (2811 * 2829) / 6800 = 1169,45 
  

• On réalise la même opération pour les onze autres cases, soit le tableau suivant : on se rend compte que pour certaines valeurs, il existe un écart conséquent avec sa valeur théorique

• À partir de là, le statisticien va utiliser la valeur de test du χ² donnée par la formule :

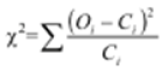
• Le test du χ² se présente comme la somme du carré des écarts entre la valeur observée et la valeur théorique. Ce carré est divisé ensuite par la valeur théorique.

• Dans cet exemple on a :

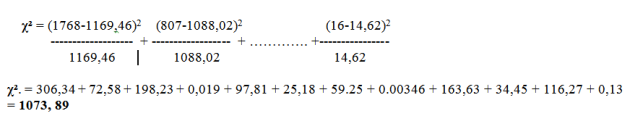
• On obtient une valeur du KHI-DEUX de 1073,89.

• Ensuite, avant de conclure, le statisticien a besoin, comme énoncé dans le paragraphe "« Fondamental »"de trois éléments complémentaires,

1.Le nombre de degré de liberté (ddl)

• Pour un test du χ², c'est le nombre de lignes et de colonnes libres, non fixés par le statisticien.

• Ici, dans cet exemple, toutes les lignes et colonnes sont libres sauf une.

• En effet, la première ligne et la première colonne sont fixées par la première valeur définie pour démarrer le test du χ². Ici, c'est 1768.

• Par conséquent, cette première ligne et cette première colonne ne sont pas libres, elle est fixée par le statisticien, contrairement aux autres.

• Ici, le nombre de ddl est de : (k lignes-1)*(L colonnes -1), soit ici, ( (3-1) * (4-1) = 6 ddl

• N.B : D'une manière générale le nombre de degré de liberté pour un test statistique est le nombre d'observations moins le nombre de paramètres à estimer entre ces observations

• le nombre de degré de liberté renseigne sur le nombre des modalités (valeurs) libres, indéterminées (non fixées a priori).

• Prenons un exemple : dans une population d'un pays X on trouve : 10 % d'actif dans le secteur primaire , 30 % d'actifs dans le secteur secondaire , 60 % dans le secteur tertiaire. Le total fait bien 100 %.

• Les deux premiers pourcentages ne sont pas fixés à priori. le troisième pourcentage dépend des deux autres. Par conséquent, les deux premiers pourcentages son libres, le troisième n'est pas libre, puisque la somme des trois valeurs doit faire 100 %.

• Ainsi, le nombre de degré de liberté est : le nombre total de modalités, ici n=3 - 1 (la troisième modalité fixée)=2 degré de liberté.

1.Le risque d'erreur α de première espèce

• Les valeurs trouvées lors de la plupart des tests statistiques sont comparées, le plus souvent, à une valeur seuil, le plus souvent fixée à 5% : c'est le seuil de signification.

• Ce risque d'erreur (risque de première espèce) représente la probabilité de rejeter l'hypothèse Ho ; « Il n'existe pas de différence significative entre la valeur du KHI-DEUX trouvée lors du calcul statistique et la valeur fournie par la table du KHI-DEUX, pour un risque de première espèce α, fixé par le statisticien à 5 %. alors qu'elle est vraie. » Ce risque de 5% est, par convention, le risque que l'on prend habituellement. Les valeurs de la table du χ² varient avec ce risque et aussi avec l' autre notion, évoqué au point 1, qu'est le nombre de degré de liberté.

• En d'autres termes, fixer un risque de première espèce α à 5 % veut dire que l'on admet une probabilité de 5 % de rejeter à tort le fait qu'il n'existe pas de différence significative entre la valeur calculée du KHI-DEUX et la valeur seuil fournie par la table du KHI-DEUX.

2.Le degré de signification ou p-value

• Nous développerons cette notion plus avant dans ce cours mais, grosso modo, le degré de signification est une probabilité servant à renforcer la conviction ou pas d'une relation statistique significative obtenue par le calcul de la valeur du χ².

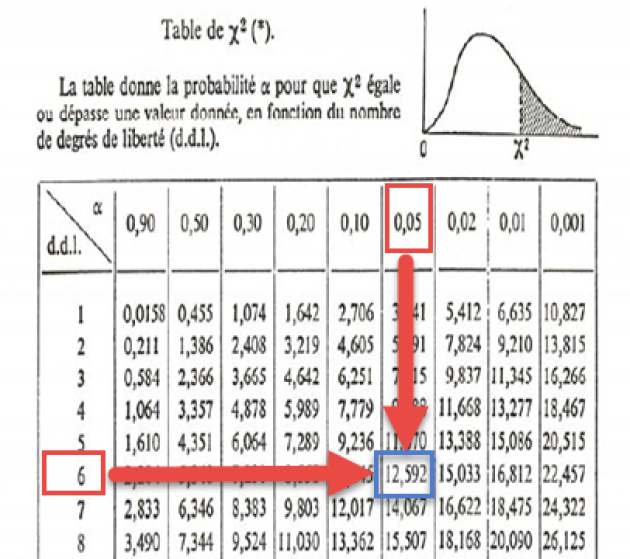
• La table du KHI-DEUX nous indique que pour un risque de première espèce α à 5 % et 6 ddl, la valeur seuil est de : = 12,592.

• On va comparer cette valeur seuil fournie par la table avec la valeur obtenue par notre calcul.

• On constate que χ² :1073, 89 largement > à = 12,592.

• Ainsi, ce test démontre une très forte corrélation ente la couleur des cheveux et la couleur des yeux dans cet échantillon de 6800 personnes

• On peut affirmer qu'il existe une forte relation statistique, c'est-à-dire un lien statistique très fort entre les deux caractères des deux variables qualitatives nominales.

• Ces deux variables ne sont, donc, pas indépendantes, mais étroitement liées. Le test vient de le démontrer scientifiquement.

Remarque

• Il est vrai que dans la pratique courante, le statisticien utilisera des logiciels spécialisés.

• Cependant, ce type de logiciel ne pourra être « manipulé » que si l'utilisateur comprend le mécanisme de chaque test statistique et sait interpréter les résultats.

Complément : La notion de degré de signification ou p value.

• Néanmoins, le statisticien, a besoin pour renforcer cette conviction de relation forte avec deux variables d'apprécier la valeur du degré de signification ou p-value.

Définition : Degré de signification ou p-value.

• Le p-value ou degré de signification ou probabilité critique observé représente « la probabilité d'observer par hasard la différence qui a été réellement observée. »

• Certains statisticiens définissent la p-value comme la plus petite probabilité, au vu des observations, de rejeter à tort l'hypothèse privilégiée Ho.

• Ainsi, de très faibles valeurs pour la p-value indiquent que l'hypothèse privilégiée Ho est peu probable.

• Plus la p-value est faible, plus les données observées témoignent que le phénomène observé a très peu de chances de se produire sous l'hypothèse nulle Ho.

• On peut, également, exprimer la définition du p-value par "le plus petit risque qu'on aurait pu prendre, tout en continuant à rejeter l'hypothèse nulle Ho"

• D'autres statisticiens affirment que le p-value représente la probabilité de ne pas rejeter Ho.

• Dans cet exemple le logiciel donne comme degré de signification p : 0.0001 soit 1 chance sur 100.000 observations de rencontrer par hasard cette différence.

• Par conséquent, cette probabilité est très très faible. Donc, ce résultat n'est pas dû au hasard. On n'accepte pas l'hypothèse Ho. En général, en statistique, on dit qu'un test est significatif lorsque la p-value < 0.05.

• D'autre part, plus la valeur du p-value est faible, plus grande sera la signification du test. Un p-value à 0.01 est plus convaincant qu'un p-value à 0.05

• Autrement dit le degré de signification ou p-value « donne un poids » à la conclusion de l'hypothèse. Le degré de signification permet de « quantifier » la force de notre conviction

Remarque sur la p-value

• le degré de signification est toujours attaché à un échantillon particulier. En changeant d'échantillon le degré de signification sera différent.

• Ainsi, on aura autant de degré de signification que d'échantillons différents.

• D'une manière générale, et pour faciliter la compréhension, on rejette systématiquement l'hypothèse Ho quand la valeur du p-value est < à 5%.

Attention : Distinction fondamentale entre le risque de première espèce alpha et le degré de signification ou p-value

• Il est fondamental, à ce stade de bien faire la distinction entre le risque de première espèce α et le degré de signification (p-value)

• En effet, même si les statisticiens ont fixé la valeur seuil de décision à 5 %, ces deux items renvoient à deux notions bien différentes.

• Le risque de première espèce α établi à 5 % (seuil de signification) est le risque que le statisticien se confère de prendre pour rejeter à tort l'hypothèse Ho

• Le degré de signification ou p-value fixé, lui aussi, à 5 % représente la probabilité de rencontrer par hasard la valeur fournit par le test du χ². C'est la probabilité réelle que la relation vérifiée soit fortuite.

• Plus cette valeur de probabilité est faible, plus cela renforce le statisticien dans la conviction que cette valeur obtenue par le calcul du χ² ne laisse rien au hasard.

• On peut sans crainte, possible, rejeter l'hypothèse Ho.

Exemple :

• Prenons le cas d'une Évaluation des Pratiques Professionnelles (EPP) sur le prélèvement sanguin par ponction veineuse réalisée en Mars 2007 temps T1 puis octobre 2008, Temps T2.

• Au temps T1, l'échantillon était de 209 Infirmières. Seules 186 observations étaient exploitables.

Au temps T2, l'échantillon était de 173 Infirmières, seules 154 observations étaient exploitables

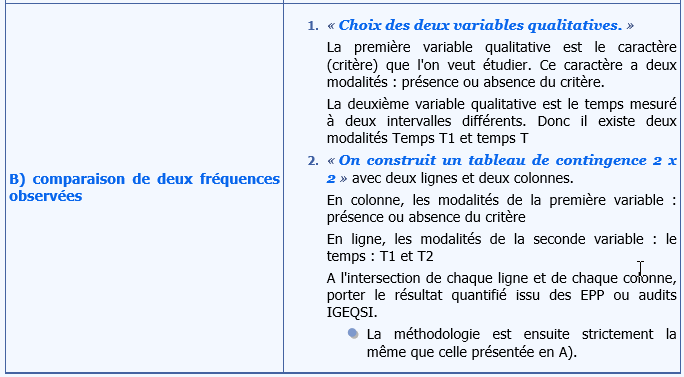
• Soit X : la première variable : « Ports de gants non stériles ». Elle admet deux modalités. La première modalité est : Port de gants non stériles. La seconde modalité est : Non port de gants non stériles.

• Soit Y : la seconde variable : « Le temps T » avec deux modalités, la première T1 : Mars 2007 la seconde : T2 Octobre 2008

• Nous allons étudier l'existence ou non d'une corrélation (relation) entre ces deux variables aléatoires qualitatives, c'est-à-dire, tester si ces deux échantillons sont homogènes ou pas pour les variables aléatoires qualitatives étudiées.

• Les statistiques de cette évaluation nous indiquent un pourcentage de ports de gants non stériles de 73 % en T1 et un pourcentage de ports de gants non stériles de 86 % en T2

• Nous allons formuler les hypothèses suivantes :

• On pose :

• L'hypothèse Ho (Hypothèse nulle) pour laquelle la différence entre les deux pourcentages :73 % et 86 % n'est pas significative au risque de se tromper de 5%. (Probabilité de rejeter l'hypothèse Ho alors qu'elle est vraie)

• L'hypothèse H1 (Hypothèse alternative) pour laquelle la différence entre les deux pourcentages :73 % et 86 % est significative.

Soit alors le tableau de contingence suivant :

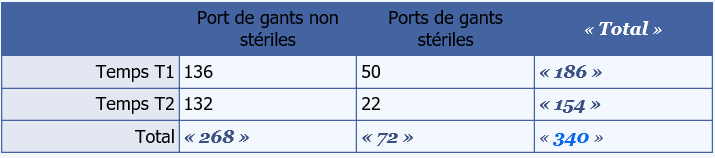
• En T1

Port de gants non stériles : 73 % de 186 IDE observées, soit 136 IDE

Pas de port de gants non stériles : 186-136 =50 IDE

• En T2

Port de gants non stériles : 86 % de 154 IDE observées, soit 132 IDE

Pas de port de gants non stériles : 154-132 =22 IDE

Attention : Conditions d'application

• Toutes les cases doivent avoir un nombre attendu théorique supérieur ou à 5. Si tel n'était pas le cas pour une case, le test ne pourrait se réaliser.

• Aussi, pour chaque case, on a vu que le calcul du nombre théorique était :

                  (total ligne*total colonne)/total général
  

• Ici, on aura respectivement :

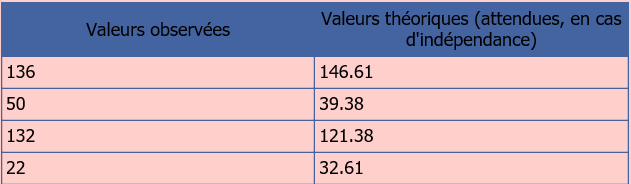
• Par conséquent, tous les valeurs théoriques sont largement supérieure à 5.

• On peut réaliser le test du χ²

• On est en présence d'un tableau de contingence dit 2 sur 2 : deux lignes et deux colonnes.

Méthode : Calcul du test du KHI-DEUX

• On rappelle la formule simple de ce test

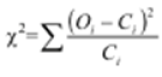
• On écrit, alors,

χ² = (136-146.61)2/146,61 + (50-39.38)2 /39.38 + (132-121.38)2 /121,38 + (22-32.61)2 /32.61 = 8,07

χ²= 8 > à = 3.84.

• En effet le nombre de degré de liberté est de (k-1)(l-1) soit 1

• Ainsi, la différence des deux pourcentages est significativement différente au risque de se tromper de 5%. On rejette l'hypothèse Ho avec un p-value < à 0.01 (probabilité de rencontrer par hasard cette différence réellement observée). Elle est faible. 1 chance sur 100 observations. Donc, ce n'est pas dû au hasard. On rejette l'hypothèse Ho.

**Attention : **

• Si on avait obtenu un test du χ²=8, mais avec un degré de signification de 0.10 par exemple cela signifierait que l'on aurait une probabilité de 10 chances pour 100 observations d'observer par hasard cette différence réellement observée.

• Par conséquent, on accepterait tout de même l'hypothèse Ho, mais avec quelques réserves sur la force de conviction d'acceptation de cette hypothèse.

Complément : Calcul automatique de la valeur du CHI-DEUX à partir d'un site Web

Calcul automatique de la valeur d'un KHI-DEUX

http://www.quantpsy.org/chisq/chisq.htm

Un autre exemple :

• Prenons un autre exemple issu de cet EPP pour lequel le χ² n'est pas significatif.

• Soit X : la première variable : « Traçabilité dans le dossier de soins ». Elle admet deux modalités. La première modalité est : Traçabilité présente. La seconde modalité est : Traçabilité absente.

• Soit Y la seconde variable : Le temps T avec deux modalités, la première T1 : Mars 2007 la seconde : T2 Octobre 2008

• Les statistiques de cette évaluation nous indiquent un pourcentage de Traçabilité présente de 82 % en T1 et Traçabilité absente de 89 % en T2.

• Nous allons formuler les hypothèses suivantes :

• On pose :

• L'hypothèse Ho (Hypothèse nulle) pour laquelle la différence entre les deux pourcentages c'est-à-dire 82 % et 89 % n'est pas significative au risque de se tromper de 5%. (Probabilité de rejeter l'hypothèse Ho alors qu'elle est vraie)

• L'hypothèse H1 (Hypothèse alternative) pour laquelle la différence entre les deux pourcentages c'est-à-dire 82 % et 89 % est significative.

• Soit alors le tableau de contingence suivant :

• En T1

Traçabilité présente: 82 % de 186 IDE observées, soit 153 IDE

Traçabilité absente: 186-153 =33 IDE

• En T2

Traçabilité présente: 89 % de 154 IDE observées, soit 137 IDE

Traçabilité absente: 154-137 =17 IDE

Attention: Conditions d'application

• Toutes les cases doivent avoir un nombre attendu théorique supérieur à 5 . Si tel n'était pas le cas pour une case, le test ne pourrait se réaliser.

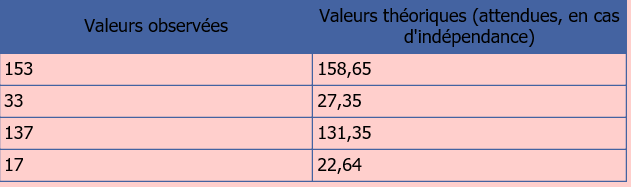
• Aussi, pour chaque case, on a vu que le calcul du nombre théorique était :

           (total ligne*total colonne)/total général
  

• Ici, on aura respectivement

Calcul du test du KHI-DEUX

• On rappelle la formule simple de ce test

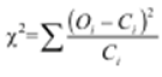
• On écrit, alors,

χ² = (153-158,65)2/158.65 + (33-27.35)2 /27.35 + (137-131.35)2 /131.35 + (17-22.64)2 /22.64 = 3,01

χ²= 3,01 < à = 3.84.

• En effet le nombre de degré de liberté est de (k-1)(l-1) soit 1

• Ainsi, la différence des deux pourcentages n' est pas significativement différente au risque de se tromper de 5%. On accepte l'hypothèse Ho avec une p-value > 0.05 (probabilité de rencontrer par hasard cette différence réellement observée).

• En effet, la p-value est > au risque de 5%. Par conséquent, cela réconforte notre conviction de ne pas rejeter Ho.

• Ainsi, l'Hypothèse Ho n'est pas rejetée au risque de se tromper de 5 %, c'est-à dire de l'accepter alors qu'en réalité cette hypothèse est fausse.

• On en conclut que les deux échantillons ne sont pas significativement différents au seuil de 5%.

Synthèse sur la méthode d'utilisation du test du χ² d'indépendance ou d'homogénéité

Simulation

Calcul automatique de la valeur d'un CHI-DEUX accompagnée du degré de signification ou p-value : p

http://quantpsy.org/chisq/chisq.htm